Продавцом предоставляются следующие гарантии:
1. Для легковых и внедорожных автомобилей BMW – гарантию на два года на весь автомобиль без ограничения по пробегу, согласно стандартам производителя Автомобиля BMW AG с момента первой регистрации Автомобиля;
Срок гарантии на дополнительное оборудование, которое не было произведено и/или установлено BMW AG, определяется согласно гарантийными условиями производителя и/или фирмы, выполняющей установку соответствующего оборудования;
· Смена владельца автомобиля не влияет на гарантийные обязательства Продавца в отношении Автомобиля, перейдите ремонт бмв.
2. Гарантия недействительна, если:
· Продавец своевременно не сообщает о дефекте или не предоставляет возможность незамедлительно устранить дефект, о котором сообщил;
· Автомобиль был перегружен, неправильно эксплуатировался или использовался для участия в соревнованиях или ралли;
· Автомобиль видоизменен таким образом, который не принимается BMW AG;
· Продавцом не были приняты во внимание инструкции и правила по эксплуатации и обслуживанию Автомобиля.
3. Гарантия недействительна и расходы не покрываются в случае естественного износа Автомобиля, а также при замене комплектующих в случае их естественного износа (шины, свечи, стеклоочистители, тормозные колодки, диски, и т. д. ). Гарантией не покрываются расходы, связанные с периодическим обслуживанием Автомобиля, регулировкой и проверками, а также с затратами или ущербом, возникшим в результате простоя Автомобиля.
4. Гарантия становится недействительной по истечении срока, указанного в 1-м пункте.
*BMW AG сохраняет за собой право вносить изменения в некоторые пункты гарантийных условий. Более подробную информацию Вы можете получить у наших специалистов по вопросам гарантии.
Продавцом предоставляются следующие гарантии:
1. Для легковых и внедорожных автомобилей BMW – гарантию на два года на весь автомобиль без ограничения по пробегу, согласно стандартам производителя Автомобиля BMW AG с момента первой регистрации Автомобиля;
Срок гарантии на дополнительное оборудование, которое не было произведено и/или установлено BMW AG, определяется согласно гарантийными условиями производителя и/или фирмы, выполняющей установку соответствующего оборудования;
· Смена владельца автомобиля не влияет на гарантийные обязательства Продавца в отношении Автомобиля, на сайте ремонт бмв.
2. Гарантия недействительна, если:
· Продавец своевременно не сообщает о дефекте или не предоставляет возможность незамедлительно устранить дефект, о котором сообщил;
· Автомобиль был перегружен, неправильно эксплуатировался или использовался для участия в соревнованиях или ралли;
· Автомобиль видоизменен таким образом, который не принимается BMW AG;
· Продавцом не были приняты во внимание инструкции и правила по эксплуатации и обслуживанию Автомобиля.
3. Гарантия недействительна и расходы не покрываются в случае естественного износа Автомобиля, а также при замене комплектующих в случае их естественного износа (шины, свечи, стеклоочистители, тормозные колодки, диски, и т. д. ). Гарантией не покрываются расходы, связанные с периодическим обслуживанием Автомобиля, регулировкой и проверками, а также с затратами или ущербом, возникшим в результате простоя Автомобиля.
4. Гарантия становится недействительной по истечении срока, указанного в 1-м пункте.
*BMW AG сохраняет за собой право вносить изменения в некоторые пункты гарантийных условий. Более подробную информацию Вы можете получить у наших специалистов по вопросам гарантии.
Р, 1955, №6
Часто применяющийся в аппаратуре дальней связи кольцевой балансный модулятор, схема которого приведена на рис. 1, в настоящее время начинает использоваться радиолюбителями-коротковолновиками для преобразования частот в диапазонных возбудителях с кварцевой стабилизацией (см. статью Л. Лабутина «Диапазонный возбудитель с кварцевой стабилизацией» в «Радио» № 5 за 1955 год). Это объясняется тем, что такой модулятор даёт на выходе наименьшее по сравнению с другими типами преобразователей количество вредных дополнительных комбинационных частот.
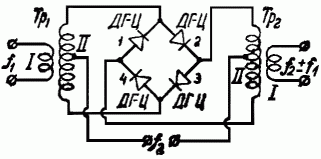
Рис. 1. Принципиальная схема кольцевого балансного модулятора
Для того чтобы понять, как работает кольцевой балансный модулятор, разберёмся сначала в том, что происходит в цепи, состоящей из генератора переменного напряжения, диода и батареи с переключателем П1, позволяющим изменять направление её включения (рис. 2, а).
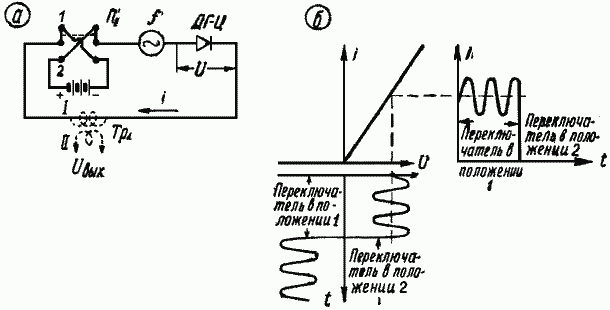
Рис. 2. а – принципиальная схема, поясняющая принцип действия кольцевого балансного модулятора; б – графическое изображение тока в цепи в зависимости от направления включения батареи.
Известно, что ток через диод может протекать только в одном направлении. Это направление называют прямым. Если напряжение батареи выбрать больше амплитуды напряжения генератора, то, когда переключатель П1 будет находиться в положении 1, в цепи потечёт пульсирующий ток, а при положении 2 переключателя П1 тока в цепи не будет (рис. 2, б). При включении в такую цепь первичной обмотки трансформатора Тр1 в его вторичной обмотке будет наводиться напряжение, пропорциональное напряжению генератора, только тогда, когда переключатель П1 установлен в положение 1. Меняя полярность включения батареи, мы изменяем сопротивление диода от некоторой малой величины Ri, зависящей от свойств диода (переключатель находится в положении 1, диод открыт), до очень большой величины (переключатель П1 установлен в положение 2, диод закрыт). В кольцевом балансном модуляторе одно из двух преобразуемых напряжений, имеющее частоту f1 подаётся на обмотку I трансформатора Тр1. Второе напряжение, имеющее частоту f2, подаётся на средние точки обмоток II трансформаторов Tp1 и Тр2 и служит для изменения сопротивления диодов. Его частота f2 должна быть больше частоты f1 На рис. 3, а и б показаны эквивалентные схемы кольцевого балансного модулятора для двух полупериодов напряжения с частотой f2. На схеме сплошными стрелками обозначено направление тока с частотой f2, а пунктирными – с частотой f1. Ток с частотой f2 не может создать напряжения в обмотке I трансформатора Тр2, так, как он протекает в половинах катушки II в разные стороны. Создать напряжение в обмотке I трансформатоpa Tp2 может ток, протекающий по обмотке II в одном направлении. Величина этого тока пропорциональна мгновенному значению напряжения с частотой f1, а направление изменяется через каждый полупериод частоты f2. На рис. 4 показаны напряжения Uf1, Uf2 и URн в случае, когда частота f2 в десять раз больше частоты f1.
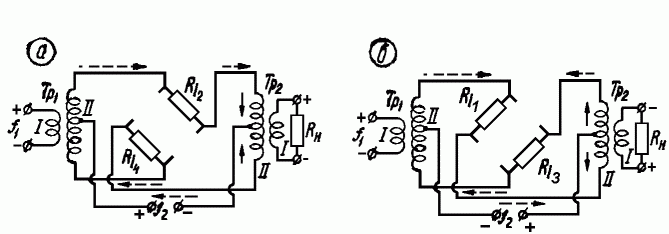
Рис. 3. Эквивалентные схемы кольцевого балансного модулятора для двух полупериодов несущей частоты
Известно, что всякую периодически изменяющуюся во времени величину, в частности и напряжение URн, можно разложить на сумму величин, изменяющихся во времени по синусоидальному закону. Для того чтобы определить амплитуды и частоты синусоидальных напряжений, из которых состоит выходное напряжение URн, нужно познакомиться с векторным изображением периодически изменяющихся во времени величин.
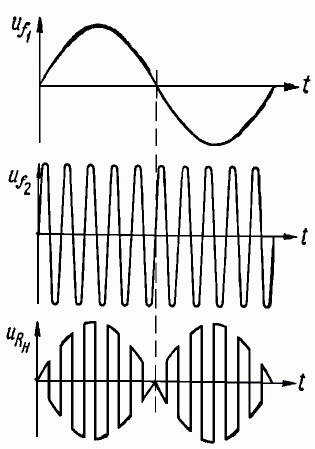
Рис. 4. Зависимость от времени преобразуемых и выходного напряжений кольцевого балансного модулятора.
Представим себе неподвижный вектор ОА, вокруг начала которого (точка О) в плоскости рис. 5, а вращается с постоянной угловой скоростью ω=2πf рад/сек прямая. Точка О делит эту прямую на положительную и отрицательную полупрямые. Величина проекции вектора ОА на эту прямую Оа будет изменяться во времени по синусоидальному закону. Проекция какого-либо другого вектора на эту же ось будет изображаться синусоидой, сдвинутой по фазе по отношению к первой. Амплитуда этой синусоиды будет равна абсолютной величине этого вектора, а сдвиг фазы в угловой мере будет соответствовать углу между векторами. Таким образом, любой изменяющейся во времени по синусоидальному закону с частотой f величине будет соответствовать неподвижный вектор, имеющий определённую величину и положение в плоскости рис. 5, а. На рис. 5, а показаны два сдвинутые на 180° вектора, имеющие одинаковую величину. Соответствующие им синусоиды показаны на рис. 5, б. На рис. 5, в показана зависимость амплитуды колебаний, или, что то же самое, величины этих векторов от времени. Таким образом, вектор OA изображает в плоскости рис. 5, а синусоидальное напряжение и с частотой f, поэтому его можно назвать «вектором величины u». Если синусоидальное напряжение модулировано по амплитуде, то величина изображающего его вектора изменяется во времени. На рис. 6 показаны модулированное напряжение и зависимость соответствующего ему изображающего вектора от времени, причём частота f2 (несущая) выбрана в десять раз больше частоты модулирующего напряжения f1, т. е. соотношение между ними такое же, как и для рис. 4. Вектор, изменяющийся во времени, можно получить, складывая вектор постоянной величины с вектором, величина и направление которого меняются (рис. 7, а). Нетрудно видеть, что период изменения его величины должен быть равен периоду модулирующей частоты f1. В свою очередь и этот вектор можно получить, складывая два равномерно вращающихся в разные стороны вектора.
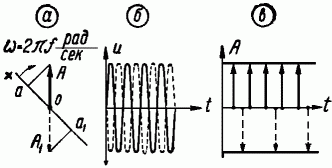
Рис. 5. Векторное изображение синусоидальных напряжений
Расположение вращающихся векторов в зависимости от времени показано на рис. 7, б. Как видно из рис. 7, а и б, за время одного периода модулирующей частоты f1 эти векторы сделают один оборот. Следовательно, вектор, поворачивающийся против часовой стрелки, будет иметь по отношению к вращающейся по часовой стрелке с угловой скоростью ω=2πf2 рад/сек прямой, угловую скорость, равную сумме их скоростей, т. е. напряжение, соответствующее этому вращающемуся вектору, будет иметь частоту, равную сумме частот несущего и модулирующего напряжений.
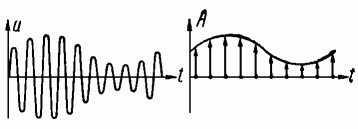
Рис. 6. Модулированное напряжение и зависимость изображающего его вектора от времени
Рассуждая таким же образом, легко увидеть, что частота напряжения, соответствующего вектору, вращающемуся по часовой стрелке, будет равна разности несущей и модулирующей частот.
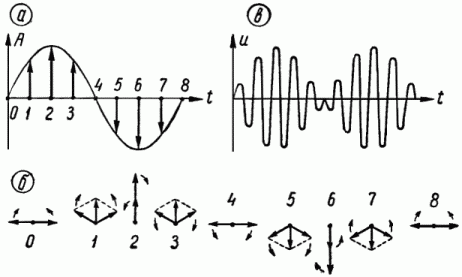
Рис. 7. Временное и векторное изображения напряжений боковых частот модулированного колебания
Таким образом, напряжение, показанное на рис. 7, в, соответствующее вектору рис. 7, а, является суммой двух синусоидальных напряжений с частотами f2+f1 и f2-f1. Это напряжение очень похоже на выходное напряжение кольцевого балансного модулятора URн (рис. 4). Некоторое различие в формах этих напряжений объясняется тем, что на выходе кольцевого балансного модулятора, кроме суммарной и разностной частот преобразуемых колебаний, имеются ещё напряжения с частотами n * f1+-f2, где n может принимать значения 3, 5, 7 и т. д. Однако эти напряжения легко могут быть отфильтрованы.
Желающие более подробно познакомиться с анализом работы кольцевого балансного модулятора могут найти интересующие их сведения в книге Н. Баева и К. Егорова «Основы дальней связи» (Связьиздат, 1948 г.).
С. Ершов